[선형대수] 04. 선형 독립(Linear Independence), 부분공간(Subspace)

슈빔멘 2021. 11. 26. 15:45

스팬이랑 부분공간은 03에서 나와야하는거 아닌가요???

흠~ 일단 그냥 하란대로 공부

정의 1.

Vector를 하나씩 추가하며 Span을 확장하는데 해당 Span이 이전 Span에 없다? => 선형 독립

반대로, 이전의 Span에서 확장이 되지 않는다? => 선형 종속(Linear Dependent)

정의 2.

Ax = b = 0 라고 가정하였을 때, x = 0인 해를 trivial solution이라함

x=0 외에도 해가 있으면 => 선형 종속

x=0 외에 해가 없으면 => 선형 독립

특징

- 선형 종속은 Span을 확장시키지 않고, 여러 개의 Solution을 가지기도 한다.

- 선형 종속은 solution이 infinite하다

- 선형 종속 : v1, v2, v3이 있고 합이 =0이라면, 두 벡터로 나머지 벡터를 만들 수 있다는 뜻이다

- 선형 독립인 경우 solution은 단 하나이다

### ? : invertible하지 않으면 해가 없거나/무수히 많았음 => 선형독립이면 그럼 invertible하다고 볼 수 있는가?

정의 : 선형 결합 아래 닫혀있는 R^n의 subset

주어진 벡터의 모든 선형결합의 집합 정도로만 생각 => ex. [0,1], [1,0]만 있으면 둘의 선형결합으로 2차원의 모든 좌표를 찍을 수 있음

(span이랑 비교할 수도 있는데 난 잘 모르겠음)

- subspace is always represented as Span => 스팬으로 부분공간을 표현할 수 있음

- 기저 Basis

부분 공간의 기저란 무엇인가

1. subspace인 H를 기저벡터(basis vector)로 모두 만들어낼 수 있어야한다.

2. 선형 독립이어야한다

두 가지를 만족하는 벡터를 기저 벡터라 한다. ex. R^2에서 [0,1], [1,0]은 기저벡터

기저 벡터는 유일하지 않다

ex. [0,3], [2,0] 얘도 기저벡터가 될 수 있음

- 차원 Dimension

=> subspace를 나타내는 기저벡터의 최소 개수

### ? : 중복 / 종속인 벡터 수도 중복으로 세나? ex. [1,0] [2,0] 있으면 2개임 1개임???????

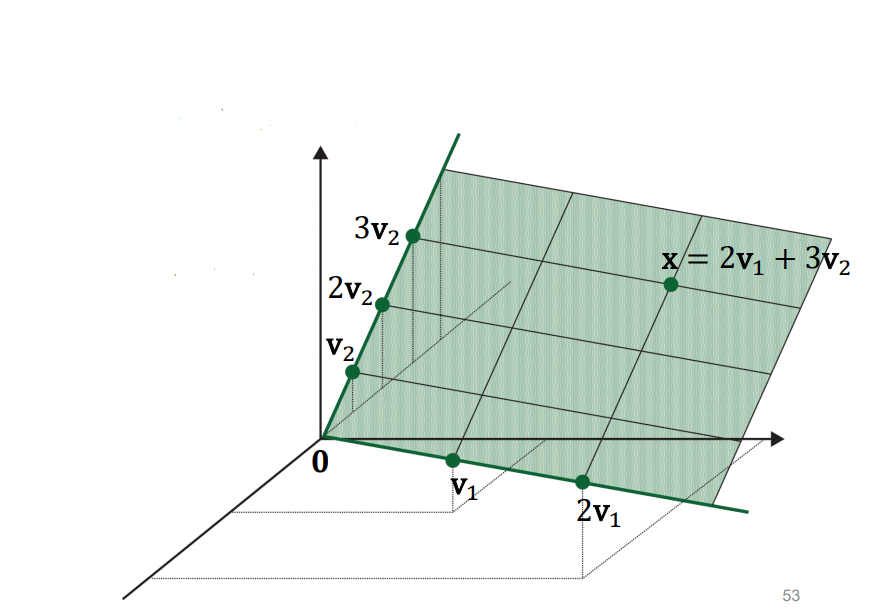
여기서의 Subspace 차원 : 평면이기 때문에 2이다 => dim 2 ^^

이것도 공간이면 공간이지 왜 또 나누는지 모르겠지만

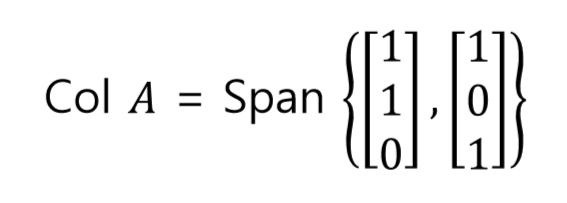
A 는 두 벡터 [1 1 0], [1,0,1]의 결합으로 만들어진다

그래서 dim Col A = 2

=> dim을 셀 때는 Column의 개수를 셈하면 된다. (중복/종속은 제거해야함)

열 공간의 차원을 랭크라 한다

그냥 단순히 rank A = dim Col A

어렵다 어려워